一文看懂深度生成模型发展脉络!从扩散模型,到流匹配再到贝叶斯流网络
近年来,扩散模型(Diffusion Models, DMs)凭借其高质量的生成能力,迅速成为AI生成领域的主流方法。然而,随着研究的深入,DMs的局限性也逐渐显现:采样效率低(需要数百甚至上千步迭代)以及对复杂模态数据(如离散数据、蛋白质结构等)的建模能力不足。为了解决这些问题,研究人员提出了两种新的生成模型——流匹配(Flow Matching, FMs)[1]和贝叶斯流网络(Bayesian Flow Networks, BFNs)[2]。这两种模型不仅在采样效率上大幅提升,还扩展了生成模型的适用范围,为新药研发、蛋白质设计、材料科学等领域带来了新的可能性。本文将帮助读者理解FMs和BFNs的工作原理,以及它们如何改进DMs。
DMs的核心思想是将复杂的生成任务分解为一系列简单的去噪任务. 通过严谨的数学推导,扩散模型的迭代去噪过程具有理论保障,并且得到了稳定、可计算的训练目标。FMs和BFNs继承了DMs的这些优势,它们同样基于“加噪-去噪”的过程,但分别从不同角度进行了改进:
- FMs:主要在加噪过程上做了改进。它将加噪过程推广为噪音和数据的中间插值,让采样过程更高效;
- BFNs:主要在去噪过程和训练过程上做了改进。它将不同模态的数据映射到一个参数空间中进行采样,能够利用数据的特点来更好地拟合分布,同时减少采样步数;
三个模型生成过程的比较如图1所示。
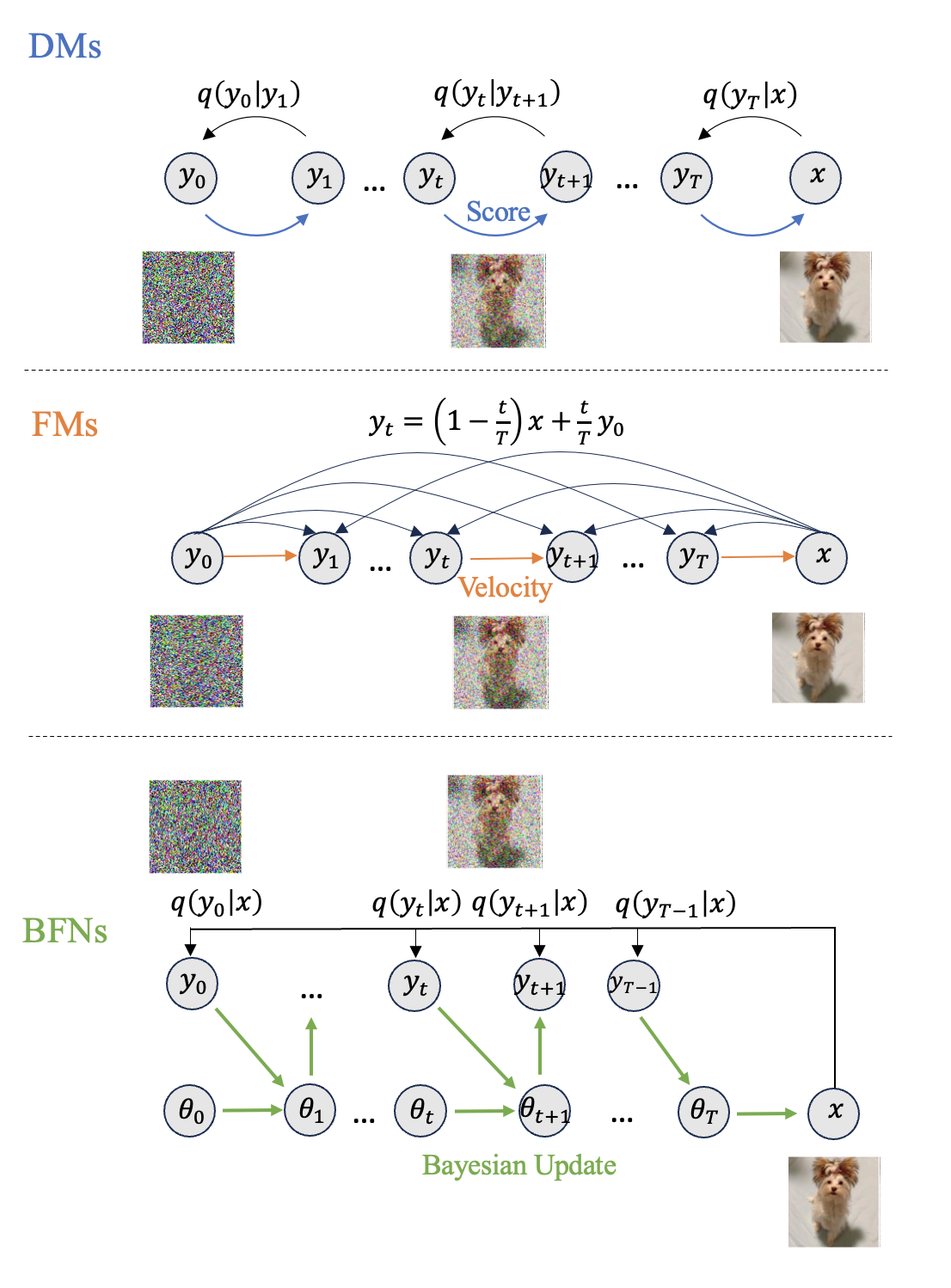
图1. DMs,FMs和BFNs的模型比较。DMs的通过马尔可夫链进行加噪,利用学习的分数函数进行去噪生成,实际上是在拟合一个逆向的微分方程。FMs通过插值来进行加噪,利用学习的速率项来逆向求解常微分方程,从而生成数据。FMs可以设计噪音与数据的相关性,来减少采样步数。BFNs从信息传递的视角,对不同时间步进行独立加噪。BFNs引入了参数空间,利用贝叶斯更新来交替进行参数更新和去噪,从而生成数据。贝叶斯更新可以适配不同数据模态,而且没有离散化误差,采样高效。
扩散模型的优势是生成质量高,可扩展,理论研究完善,在有足够计算资源的情况下可以生成高质量样本,在图像和视频生成中仍是SOTA[3-5]。
FMs的优势是加噪过程灵活,采样效率高。劣势是需要训练时需要额外计算,来保证采样效率。FMs适合高效生成的任务。在图片[6],语音[7]和视频[8]生成中FMs都可以使用更少的采样步数达到匹配SOTA的效果。进一步,利用reflow和蒸馏,FMs可以实现一步图片生成[9]。
BFNs的优势是支持多模态数据,引入数据本身的归纳偏置来提升建模能力,并且无离散化误差。但是训练过程较为复杂,且需要较多的理论推导来得到采样公式。BFNs适用于生成复杂模态数据。目前,BFNs已成为多个科学领域的数据生成SOTA,包括小分子生成[10],基于结构的药物设计(SBDD)[11],蛋白质设计[12]以及材料晶体设计[13]等。几个模型的对比如下表所示。
| DMs | FMs | BFNs | |
|---|---|---|---|
| 加噪过程 | 随机微分方程+马氏链 | 任意噪声+数据-噪声耦合 | 复杂模态适配+参数空间 |
| 采样效率 | 低(需数百步) | 高(可一步生成) | 中高(无离散化误差) |
| 适用数据 | 连续数据(图像、视频) | 连续/离散/流形数据 | 复杂模态数据(离散、图、几何) |
| 理论框架 | 微分方程(SDE+ODE) | 常微分方程(ODE) | 贝叶斯更新+参数空间 |
| 应用场景 | 高保真图像生成 | 实时生成、高效生成 | 科学数据生成(药物、蛋白质、材料等) |
DMs、FMs和BFNs的综合对比
接下来,我们将从加噪过程、采样过程(去噪过程)和训练过程三个方面,详细对比DMs、FMs和BFNs的区别和优势。通过这种对比,我们可以更清楚地看到FMs和BFNs如何改进DMs,并在实际应用中发挥更大的作用。
加噪过程
DMs,FMs和BFNs的底层思路是类似的,都构造了一系列带噪样本 \(y_1,y_2,\cdots,y_n\) 来将目标数据\(x\)转化为噪音,再使用神经网络来逆转这个过程,将噪音转化为数据。为了加噪过程可逆,DMs采用随机微分方程方程进行加噪。FMs基于常微分方程,提出了一种更一般的加噪过程,允许更多的噪音类型以及数据和噪音耦合,可以加速生成。BFNs则从信息传输的视角来加噪,只需设计带噪样本的信噪比,减少了设计负担:
| 加噪过程 | ||
|---|---|---|
| DMs | DMs使用SDE对数据加入高斯噪音: \(y_t=f_ty_tdt+g_tdw,t\in[0,T]\) | * 加噪过程收到SDE形式的局限 |
| FMs | 条件流的加噪方式:\(y_t=(1-t)x+t\epsilon, t \in[0,1]\) | * 中间插值,可以适配不同噪音和数据类型 * 允许数据和噪音的耦合 |
| BFNs | 发送者分布: \(q_S(y_1,y_2,⋯,y_n\mid x)=\prod^n_{i=1}q_S(y_i∣x,\alpha_i)\) | * 信息传输的新视角 * 简化了加噪过程的设计 * 可以适配不同数据模态 |
DMs:马尔可夫链加噪
DMs的加噪过程也被称为前向过程(Forward Process),一般可以用一个随机微分方程(SDE)来描述:
\[y_t=f_ty_tdt+g_tdw,t \in [0,T]\]其中\(y_0=x\sim q_{data}\left(x\right)\),即目标数据,\(y_T\sim\mathcal{N}\left(0,I\right)\),即无信息的标准高斯分布,\(y_t\)的噪音强度随t增大而增大。dw是无穷小的高斯噪音(布朗运动),\(f_t\),\(g_t\)是两个提前确定的函数,它们规定了前向过程如何进行加噪,一般来说\(f_t\),\(g_t\)与\(y_t\)无关,仅与t相关
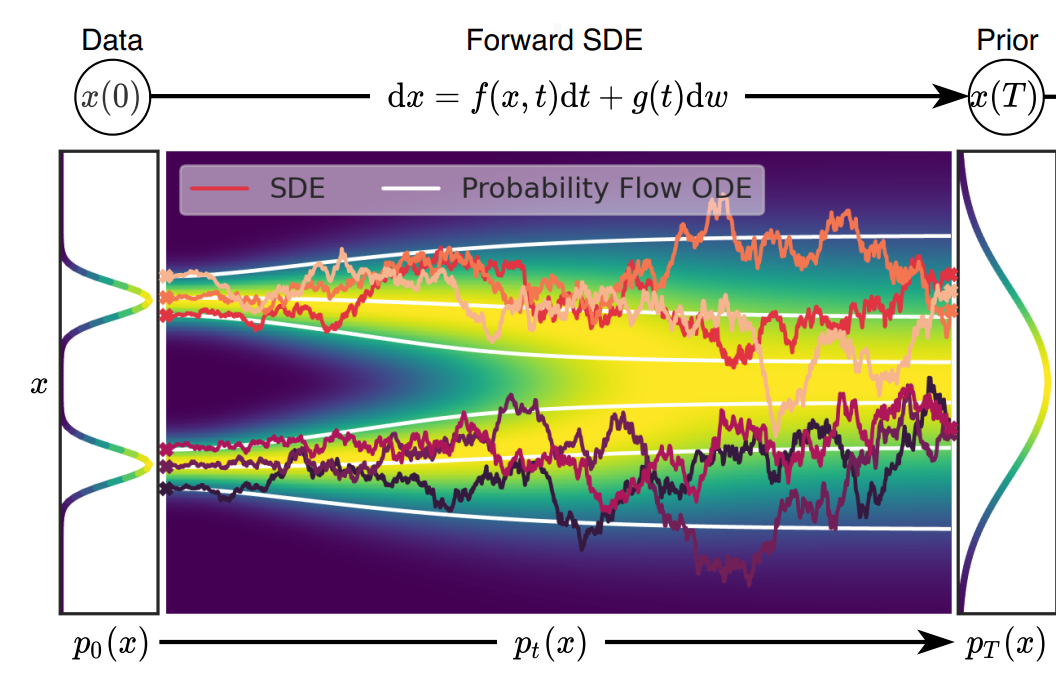
图2. SDE视角下的DMs前向过程(来源:Song yang et al. [14])
公式(1)提供了一个统一的理论视角。实际应用中会对前向过程进行离散化,得到\(y_1,y_2,\cdots,y_n\)的分布:
\[q(y_1,y_2,\cdots,y_n | x)=q(y_1|x)\prod_{i=1}^{n}q(y_{i+1}|y_i)\]例如,\(y_{i+1}=f_ty_t\mathrm{\Delta t}+\ g_t\sqrt{\mathrm{\Delta t}}\epsilon_t\sim q\left(y_{i+1}\mid y_i\right), \mathrm{\Delta t}\)是离散化的步长。根据\(f_t\),\(g_t\)的选择和不同的离散方式,可以得到DDPM (Denoising Diffusion Probabilistic Models),DDIM(Denoising Diffusion Implicit Model)或 NCSN (Noise-Conditioned Score Network) 等不同的扩散模型。
DMs的特点是向数据中加入高斯噪音,然后根据实现确定的加噪规则创造\(y_1,y_2,\cdots,y_n\)的 马尔可夫链。问题在于,高斯噪音并不一定是最好的噪音选择,因为它没有考虑具体的数据特点;另外我们并不一定需要马尔可夫链来进行加噪,我们只需要一个噪音强度逐渐变化的可逆过程。
FMs:中间插值加噪
为了扩展加噪过程,FMs将加噪过程设计为真实数据和噪音的中间插值:
\[y_t=(1-t)x+t\epsilon, t\in[0,1]\]其中\(x\)是真实数据,\(\epsilon\)是任何一种噪音,\(y_t\)是加噪后的样本,当t从0增加到1时,\(y_t\)从真实数据逐渐变化为纯噪音。
注意, \(\epsilon\)的类型可以根据数据模态进行设计,如建模离散数据时\(\epsilon\)可选为狄利克雷分布,也可以扩展到黎曼流形上的数据,从而适配不同数据模态。
进一步,FMs的加噪过程允许x和\(\epsilon\)是相关的,即\(q\left(x,\epsilon\right)\neq q\left(x\right)q\left(\epsilon\right)\)。\(q\left(x,\epsilon\right)\)也被称为数据与噪音的耦合(coupling)。为了加速生成,可以使用近似的最优传输耦合\(\pi\left(x,\epsilon\right)\)(Optimal Transport Coupling),理论上最优传输耦合下\({\{y}_t\}_{t\in\left[0,1\right]}\)的轨迹是一条条互不交叉的直线,利用直线的斜率就可以实现一步生成。但是注意,FMs本身无法保证轨迹是直线,只有进行耦合后轨迹才会“变直”,事实上若\(\epsilon\)是高斯噪音且不进行耦合,FMs和DMs是等价的。
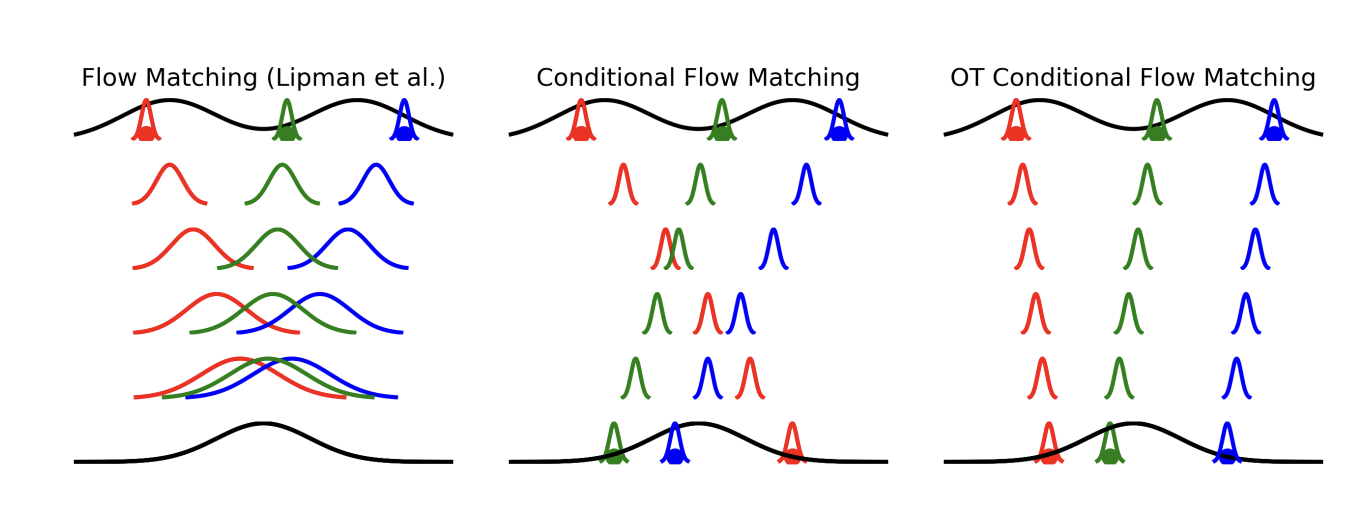
图3. 如最右图所示,采用最优传输耦合后,数据与噪音由不交叉的直线连接,理论上可以进行一步生成(来源:Tong et al.[15])
公式(3)是FMs的一个特例。FMs一般的加噪过程是条件在下的常微分方程(ODE):
\[\frac{dy_t}{dt}=u_t(y_t|x), t\in[0,1]\]其中 \(u_t\left(y_t\mid x\right)\) 是任何可以将x转变为\(\epsilon\)的速率场,如公式(3)中, \(u_t\left(y_t\mid x\right)=\frac{x-y_t}{1-t}\) . 公式(4)是条件在真实x下的条件流,分布可以记为 \(p\left(y_t\mid x\right)\),对x的分布进行积分就得到了由条件流导出的边缘(marginal)流:
\[p\left(y_t\right)=\int{p\left(y_t\mid x\right)}q_{data}\left(x\right)dx\]\(y_t\)来自于边缘ODE:
\[\frac{dy_t}{dt}=u_t(y_t), t\in[0,1]\]其中\(u_t\left(y_t\right)=\int^{u}_t\left(y_t\mid x\right)\frac{p\left(y_t\mid x\right)q_{data}\left(x\right)}{p\left(y_t\right)}dx\)
BFNs:独立加噪
BFNs采用了信息传输的视角,发送者(sender)发出带噪音的信息,接受者(receiver)利用带噪信息来更新分布。这个视角下,前向过程简化为发送一系列带噪样本信息。带噪样本是由发送者分布(sender distribution)得到的:
\[q_S\left(y_1,y_2,\cdots,y_n|\ x\right)=\prod_{i=1}^{n}{q_S\left(y_i\mid x,\alpha_i\right)}\]其中\(q_S\)是已知形式的发送者分布,超参数\(\alpha_i\)决定了发送者分布的信噪比。\(\alpha_i\)关于i是单调递增的,信噪比逐渐趋于1。
对比DMs,BFNs的带噪样本分布不需要马尔可夫性,只需要确定每个带噪样本的信噪比,简化了前向过程的设计复杂度。此外,BFNs会根据变量类型来选择\(p_s\),例如:
- 连续型变量的\(p_s\)为\(\mathcal{N}\left(x,\alpha^{-1}I\right)\)
- 离散型变量的\(p_s\)为\(\mathcal{N}\left(\alpha\left(Ke_{x}-1\right),\alpha KI\right)\),其中K是离散类比总数,\(e_x\)是\(x\)的one-hot表示。
这样的设计是为了后续贝叶斯推断的统一数学框架,并简化采样过程中的数学计算。
采样过程
DMs和FMs的采样过程很相似,都是利用神经网络作为微分方程的速率项,模拟逆向的微分方程来生成样本。而BFNs则相对复杂。为了适配更为复杂的多模态数据,BFNs引入了一个参数空间,并在这个参数空间上进行带噪信息的整合利用以及去噪,两者区别如图2所示。

图2. BFNs与DMs采样过程的概率图模型(来源:Song et al.[10])
| 采样过程 | ||
|---|---|---|
| DMs | 使用数值计算来拟合逆向SDE: \(y_{t+\Delta t}= (f_ty_t-g_t^2s_\theta(y_t,t))\Delta t+ g_t\sqrt{\Delta t}\epsilon_t\) 其中 \(s_\theta(y_t,t)\) 是学习的分数函数,\(\Delta t\) 是离散化步长 |
* 采样步数多,受离散化误差影响 * 分数函数在复杂模态上难以定义 |
| FMs | 使用数值计算来拟合逆向ODE:\(y_{t+\Delta t} = y_t+\Delta tv_\theta(x_t,t)\) 其中\(v_\theta(x_t,t)\)是学习的速率函数 |
* 轨迹更直,采样更快 * 仍受离散化误差影响 |
| BFNs | 基于贝叶斯更新公式进行迭代生成:\(\theta_i=h(\theta_(i-1),\hat{y}_i, \alpha_i), \hat{y}_i\sim p_R(y_i∣\theta_(i-1),i-1,\alpha_i)\) | * 无离散化误差,采样快 * 支持多模态数据,利用数据特性的归纳偏置 |
DMs:拟合逆向SDE
DMs的采样过程是公式(1)的逆过程,即一个逆向SDE:
\[y_t=\left(f_ty_t-{g_t}^2\mathrm{\nabla}_ylog{p_t}\left(y_t\right)\right)dt+g_td\bar{w}\]其中\(\bar{w}\)是逆向的布朗运动。在公式(7)中,唯一的未知量就是\(\nabla_y\log{p_t}\left(y_t\right)\),被称为分数函数(Score Function)。扩散模型使用神经网络\(s_\theta\left(y_t,t\right)\)来拟合分数函数。将训练好的\(s_\theta\left(y_t,t\right)\)带入到上述SDE中,并使用数值计算方法来求解公式(5),就可以生成数据:
\[y_{t+\mathrm{\Delta t}}=\ \ \left(f_ty_t-{g_t}^2s_\theta\left(y_t,t\right)\right)\mathrm{\Delta t}+\ g_t\sqrt{\mathrm{\Delta t}}\epsilon_t\]上述公式是利用一阶的Euler–Maruyama方法的采样方法,\(\mathrm{\Delta t}\)是离散步长,\(\epsilon_t\)是标准高斯噪音。通常来讲\(\mathrm{\Delta t}\) 需要足够小,才能较好地拟合公式(7)。
公式(7)也可以等价的(保证生成数据的分布不变)转化成ODE形式:
\[y_t=\left(f_ty_t-\frac{1}{2}g_t^2\mathrm{\nabla}_ylog{p_t}\left(y_t\right)\right)dt\]为了在保持质量的条件下减少采样步数,可以使用高阶的数值求解器或者设计积分求解器来进行生成。
然而,DMs难以处理离散型数据或具有离散结构的数据,其本质原因是分数函数在这种离散空间上没有良好定义。此外,DMs的采样效果受离散化误差的影响,当采样步数较少时,就难以精确拟合SDE,降低生成样本的质量。
FMs:拟合逆向ODE
类似DMs,FMs的目标是逆向求解公式(5)。FMs利用神经网络\(v_\theta\left(x_t,t\right)\)来估计公式(5) 中的Velocity项,即\(u_t\left(y_t\right)\),并利用Euler算法等数值计算方法来逆向求解:
\[y_{t+\mathrm{\Delta t}}=y_t+\mathrm{\Delta t}v_\theta\left(x_t,t\right)\]类似的,FMs也有离散化误差,同样也可以利用高阶的数值求解器来减少离散化误差对样本质量的影响。使用OT coupling,理论上最优的\(v_\theta\)是与t无关的常数,所以只需要进行一步计算即可( \(\mathrm{\Delta t}=1\) ). 但是OT coupling一般需要大量的额外计算,因为求解高维的最优传输问题本身就极为困难。
BFNs:迭代贝叶斯更新
为了解决DMs在复杂模态数据上的问题以及离散化误差的问题,BFNs利用贝叶斯更新在参数空间进行采样。BFNs的采样过程从先验参数\(\theta_0\)开始,利用带噪信息\({y_1,y_2,\cdots,y_n}\)来迭代地更新参数\(\{\theta_0,\theta_2,\cdots,\theta_{n-1}\}\)。在信息传递的视角下,接收者的先验信息是\(\theta_0\),然后接收带噪信息并更新\(\theta\),如下图所示。
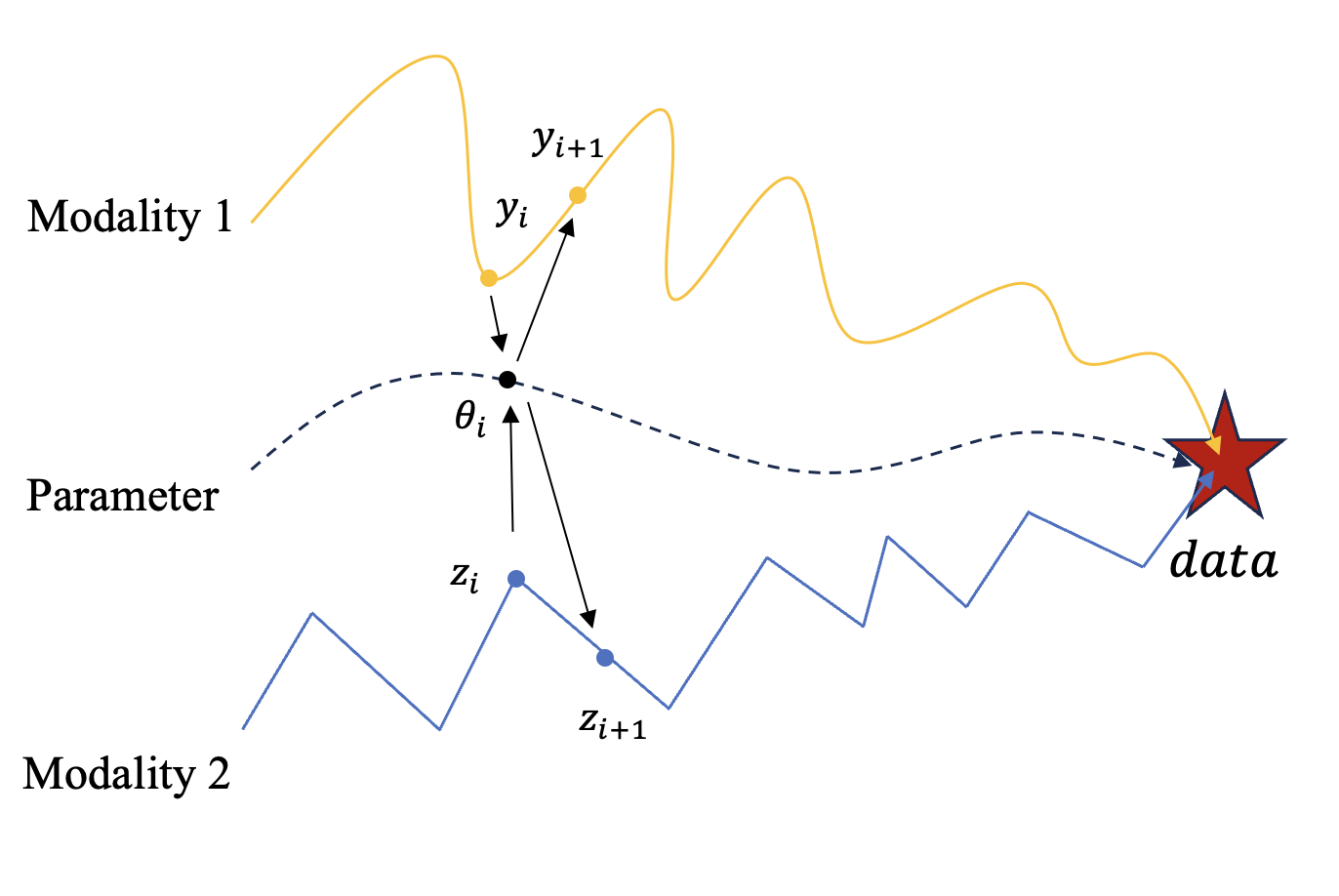
图4. BFNs的带噪信息轨迹和参数轨迹。在BFNs中,不同模态的带噪信息都会映射到一个连续的参数空间中,用来更新参数;然后BFNs会基于更新后的参数整合不同模态信息,并对数据空间中的带噪信息进行去噪。
BFNs的参数空间
首先,我们介绍BFNs构造的参数空间:
\[p_I\left(x\right|\theta)=\ \prod_{d=1}^{D}p_I\left(x^{\left(d\right)}|\theta^{\left(d\right)}\right)\]\(p_I\left(x\right|\theta)\)被称为输入分布(Input Distribution),是已知的先验分布。\(\theta\)是输入分布的参数,BFNs将在这个参数空间上进行学习以及生成。这种贝叶斯的视角为BFNs提供了本质上的改进:我们可以根据数据特点选择合适的输入分布:
- 对于连续数据,\(p_I(x\mid\theta)\) 可取为高斯分布,\(\theta\) 即为高斯分布的期望与方差
- 对于离散数据 \(p_I\) 可取为Categorical分布,\(\theta\) 是每个类别的概率。
进一步,BFNs可以对图数据甚至周期性数据设计先验分布和参数。利用数据特性的inductive bias,BFNs可以更好的拟合复杂数据的分布。
贝叶斯更新
假设参数为\(\theta_{i-1}\),接受到了带噪信息\(y_i\),BFNs利用贝叶斯更新函数h得到\(\theta_i\):
\[\theta_i=h\left(\theta_{i-1},y_i,\ \alpha_i\right)\]h是一个确定的函数,\(\alpha_i\)是发送者分布的精度参数。h具体形式由数据模态决定:
- 对于连续型数据,输入分布是高斯分布:\(p_I\left(x\right|\theta_{i-1},)=\mathcal{N}(x|\mu_{i-1},\rho_{i-1}^{-1})\) \(\rho_{i-1}\)表示分布的精度,\(\mu_{i-1}\)是分布的均值。贝叶斯更新函数为:
其中 \(\rho_i=\rho_{i-1}+\alpha_i, \mu_i=\ \frac{\mu_{i-1}\rho_{i-1}+y_i\alpha_i}{\rho_i}\)
在获取信噪比为\(\alpha_i\)带噪信息后,参数的精度增加了\(\alpha_i\),而均值会根据带噪信息和上一步的均值进行加权求和。
- 对于离散型数据,输入分布是Categorical分布,\(\theta\)满足\(\sum_{k}\theta_k=1\),其中\(\theta_k\)表示先验参数\(\theta\)的第k个分量。贝叶斯更新函数为:
\({h(\theta_{i-1},y_i,\alpha_i)}_j\)表示更新后参数的j个分量。直观来看,带噪信息用来对\(\theta_{i-1}\)进行重新归一化,归一化因子是\(e^{y_i}\)。
根据\(p_S\)以及公式(8)可以得到条件在\(\theta_{i-1}\)下\(\theta_i\)的分布:
\[p_u\left(\theta_i|\theta_{i-1},\alpha_i\right)=\ \mathbb{E}_{p_s\left(y_i| x,\alpha_i\right)}\delta\left(\theta_i-h\left(\theta_{i-1},y_i,\alpha_i\right)\right)\]其中\(\delta\)是狄拉克delta函数,\(p_u\)也被称为贝叶斯更新分布(Bayesian Update Distribution)。利用贝叶斯更新的马尔科夫性,可以得到参数轨迹\(\theta_0,\theta_2,\cdots,\theta_{n-1}\)的分布:
\[p\left(\theta_0,\theta_2,\cdots,\theta_{n-1}\right)=\prod_{i=1}^{n-1}{p_u\left(\theta_i|\theta_{i-1},\alpha_i\right)}\]其中\(\theta_0\)是确定的先验参数。
相比于DMs,BFNs可以引入符合数据特性的归纳偏置(Inductive Bias)。例如,离散变量的生成中,BFNs可以保证生成的轨迹总是在概率单纯形内,在图2展示了离散变量K=3时,BFNs采样的参数轨迹。对于 K = 3 的情况,输入分布参数 \(\theta=\left(\theta_1,\theta_2,\theta_3\right)\)可以可视化为 2-单纯形上的点,初始时\(\theta_1=\theta_2=\theta_3=1/3\), 数据 x 对应于左下角。可以看到,由于\(\theta\)满足\(\sum_{k}\theta_k=1\),参数轨迹总是在概率单纯形内,并且最终收敛到真实数据。
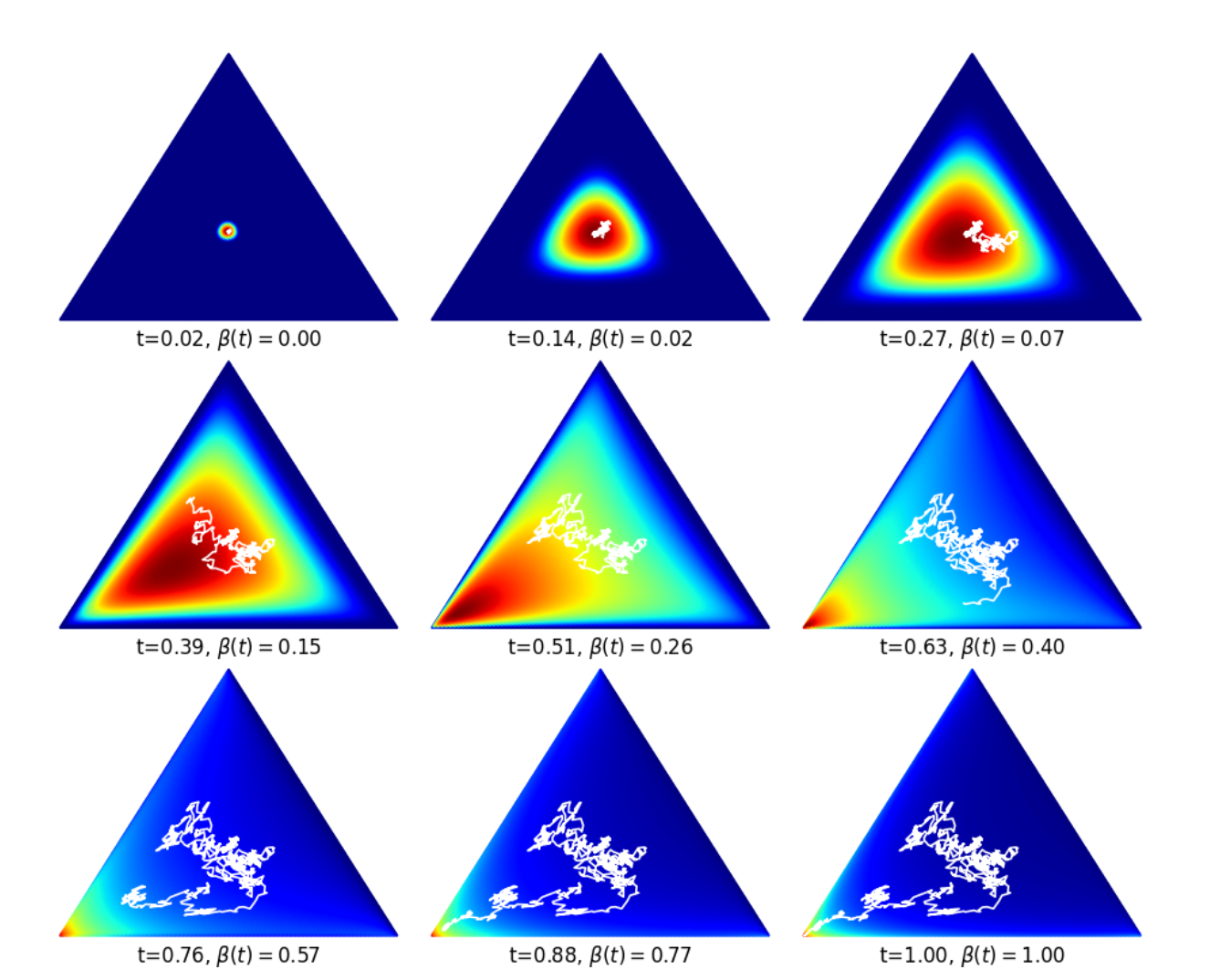
图2. 离散数据的参数轨迹(来源:Graves et al. [2])
BFNs中神经网络的作用
BFNs的采样过程需要发送者分布(公式(6))提供的带噪信息。然而,采样过程中无法直接使用发送者分布,因为真实的x是未知的。所以BFNs采用了一种变分的方法,训练神经网络来预测原始数据x,然后将预测的数据输入发送者分布加噪,得到预测的y,如下图所示。
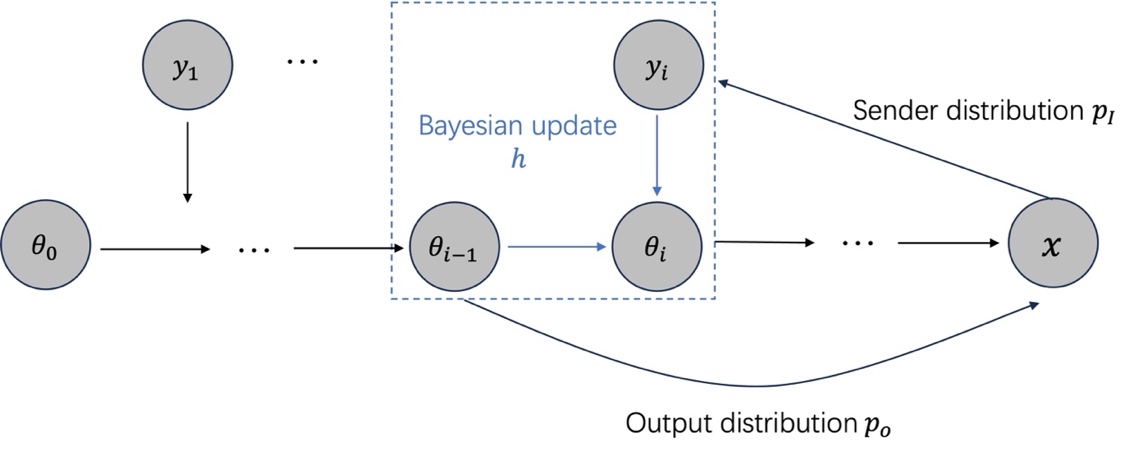
图3. BFN的采样过程
具体来说,BFN的使用神经网络参数化了一具体来说,BFN的使用神经网络参数化了一个输出分布(Output Distribution)来预测x:
\[p_O\left(x|\theta_i,i\right)=\ \prod_{d=1}^{D}{p_O\left(x^{\left(d\right)}|\Phi^{\left(d\right)}(\theta_i,i)\right)}\]其中\(\Phi\)是神经网络,其输入是连续参数\(\theta_i\),输出是\(p_O\)的参数。\(p_O\)可以根据数据模态来选取:
- 连续数据,\(p_O\left(x\mid\theta_i,i\right)=\Phi\left(\theta_i,i\right)\),即\(p_O\)为delta 分布
- 离散数据,\(p_O\left(x\mid\theta_i,i\right)=Softmax\left(\Phi\left(\theta_i,i\right)\right)\),保证\(p_O\)的输出仍在概率单纯形内
值得注意的是,BFNs的神经网络是在参数空间中工作的,其输入和输出都是分布的参数。连续的参数空间蕴涵了各个模态的信息,可以为神经网络提供更丰富的信息,提高预测性能;并且不需要额外约束神经网络的形式。 基于输出分布,BFN推导出了接收者分布(Receiver Distribution),作为发送者分布的近似:
\[p_R\left(y_i|\theta_{i-1},i-1,\alpha_i\right)=\ \mathbb{E}_{p_O\left(x|\theta_{i-1},i-1\right)}p_S\left(y_i| x;\alpha_i\right)\]直观来看,BFNs将预测的\(x\)输入发送者分布中得到预测的\(y_i\),并对所有可能的\(x\)进行加权积分,得到了对\(y_i\)的估计。在采样过程中,BFNs迭代地利用\(p_R\)来更新参数,如图3所示:
\[\theta_i=h\left(\theta_{i-1},{\hat{y}}_i,\ \alpha_i\right),\ \ {\hat{y}}_i\sim p_R\left(y_i|\theta_{i-1},i-1,\alpha_i\right)=\ \mathbb{E}_{p_O\left(x|\theta_{i-1},i-1\right)}p_S\left(y_i| x;\alpha_i\right).\]根据BFNs的采样过程可以看出,BFNs不受离散化误差的影响,因为贝叶斯更新的计算不涉及到离散化(h的形式是直接根据贝叶斯公式推导出来的)。这意味着BFNs可以使用更少的步数进行采样。
训练过程
基于微分方程的加噪-去噪过程,DMs和FMs的设计训练目标的思路是类似的:构造一个条件的训练目标,使得网络在拟合这个条件目标时可以获得与拟合真实目标相同的梯度。另一方面,为了统一处理不同模态数据的生成,BFNs直接拟合带噪样本与真实带噪样本的分布差异:
| 训练过程 | ||
|---|---|---|
| DMs | 去噪分数匹配: \(E_t\lambda(t)E_{p_{data},p(y_t\mid x),}\parallel ∇_y{\rm log}p_t(y_t\mid x)-s_\theta(y_t)\parallel^2_2\) 等价的\(\epsilon\)-预测: \(E_{p_{data},p_{noise}}\parallel \epsilon-\epsilon_\theta(y_t)\parallel ^2_2\) |
* \(L_2\) 可稳定计算,理论保证完善 * 权重 \(\lambda(t)\) 对于生成效果有较大影响,需要设计 |
| FMs | 条件流匹配: \(E\lambda(t)E_{p(x,y_t)}\parallel u_t(y_t\mid x)-v_\theta(y_t)\parallel^2_2\) | * \(L_2\) 损失可稳定计算 * 需要额外拟合耦合分布,增加训练复杂度 |
| BFNs | 拟合带噪样本分布: \(\sum^n_{i=1}E_qD_{KL}(p_\phi(⋅\mid \theta_(i-1))\parallel q(⋅\mid x)) -E_{y_1⋯,y_n\sim q}{\rm log}p_\phi(x\mid \theta_n)\) 连续时间: \(L^\infty(x)=E_{p_F(\theta_t\mid x,t)}\alpha(t)\parallel x-E_{p_o(\hat{x}\mid \theta_t)}\hat{x}\parallel_2^2\) |
* KL散度导致训练不稳定 * \(L^\infty\) 计算稳定高效,但是是 \(n\) 趋于无穷时的近似损失 |
DMs:去噪分数匹配
| DMs的训练目标是\(\mathrm{\nabla}_ylog{p_t}\left(y_t\right)\),由于其本身涉及到对\(p_{data}\)的卷积,所以难以计算。扩散模型使用去噪分数匹配来训练,将条件分数函数$$\nabla_y\log{p_t}\left(y_t | x\right)$$作为训练目标: |
可以证明优化这个目标所获得的梯度等价于直接拟合分数函数。其中\(\lambda\left(t\right)\)是权重,可以证明一定权重下这个目标是负对数似然的变分上界,为扩散模型的表现提供了理论保障。
根据前向过程的定义可以将\(\nabla_y\log{p_t}\left(y_t\mid x\right)\)化简,因为\(p_t\left(y_t\mid x\right)\)就是高斯分布。化简后可得到常用的\(\epsilon\)-预测:\(E_{p_{data},p_{noise}}{\parallel\epsilon-\epsilon_\theta\left(y_t\right)\parallel ^2}_2\),或\(x\)-预测\(E_{p_{data},p_{noise}}{\parallel x-x_\theta\left(y_t\right)\parallel ^2}_2\)。上述不同的参数化在相差一个权重意义下是等价的,但是这个权重对于最终的生成效果影响很大,导致在不同领域中预测目标的选择也不同。
FMs:速率匹配
类似于DMs,FMs的训练目标是\(u_t\left(y_t\right)\),然而\(u_t\left(y_t\right)\)的表达式涉及到\(q_{data}\left(x\right)和p\left(y_t\right)\), 所以难以直接计算。借鉴了DMs的条件训练方法,FMs将容易计算的条件速率\(u_t\left(y_t|x\right)\):
\[{L=E_t\lambda\left(t\right)E}_{p\left(x,y_t\right)}{\parallel u_t\left(y_t|x\right)-v_\theta\left(y_t\right)\parallel ^2}_2\]FMs证明了优化这个目标获得的梯度等价于直接拟合\(u_t\left(y_t\right)\)。
若使用OT-coupling或其他耦合策略,则需要先拟合\(p\left(x,y_t\right)\),然后从拟合的耦合分布中采样训练batch,然后计算损失和梯度。
BFNs:拟合带噪分布
训练目标
由上一节内容可知,BFNs的神经网络的作用是提供好的带噪样本以进行贝叶斯更新。我们用\(p_\phi\)表示神经网络拟合的分布,BFNs的损失函数为真实的带噪样本分布和生成的分布的差异:
\[L\left(x\right)=-E_{y_1\cdots,y_n\sim q}[log\frac{p_\phi\left(y_1\cdots,y_n,x\right)}{q\left(y_1\cdots,y_n| x\right)}] \\\\ {=-\ E}_{y_1\cdots,y_n\sim q}[log\frac{p_\phi\left(y_1\cdots,y_n\right)}{q\left(y_1\cdots,y_n| x\right)}] - {\ E}_{y_1\cdots,y_n\sim q}logp_\phi\left(x|y_1\cdots,y_n\right) \\\\ =^{\left(1\right)}{-E}_{y_1\cdots,y_n\sim q}[log\frac{\prod_{i=1}^{n}{p_\phi\left(y_i|\theta_{i-1}\right)}}{q\left(y_1\cdots,y_n| x\right)}] -{\ E}_{y_1\cdots,y_n\sim q}logp_\phi\left(x|y_1\cdots,y_n\right)\\\\ {=^{\left(2\right)}-E}_{y_1\cdots,y_n\sim q}[log\frac{\prod_{i=1}^{n}{p_\phi\left(y_i|\theta_{i-1}\right)}}{q\left(y_1\cdots,y_n| x\right)}] -{\ E}_{y_1\cdots,y_n\sim q}logp_\phi\left(x|y_1\cdots,y_n\right)\\\\ =\ {-E}_{y_1\cdots,y_n\sim q}[log\frac{\prod_{i=1}^{n}{p_\phi\left(y_i|\theta_{i-1}\right)}}{\prod_{i=1}^{n}q\left(y_i|x\right)}] -{\ E}_{y_1\cdots,y_n\sim q}logp_\phi\left(x|y_1\cdots,y_n\right) \\\\ =\sum_{i=1}^{n}{E_qD_{KL}(p_\phi(\cdot|\theta_{i-1})||\ q(\cdot|x)){\ -E}_{y_1\cdots,y_n\sim q}}logp_\phi\left(x|\theta_n\right) \\\\ =L^n\left(x\right)+L^r\left(x\right)\]其中等号(1)是因为采样过程中的带噪样本分布可以分解为接收者分布\(p_\phi\left(y_i\mid \theta_{i-1}\right)\)的迭代,等号(2)是因为在最后一步中,输出分布仅利用了\(\theta_n\)。最后得到的\(L^n\left(x\right)\)表示拟合带噪样本分布的损失,也可以理解为一种信号传输损失,\(L^r\left(x\right)\)是重构损失。
此外,\(-L\left(x\right)\)是对数似然的变分上界:
\[-L\left(x\right)=E_{y_1\cdots,y_n\sim q}[log\frac{p_\phi\left(y_1\cdots,y_n,x\right)}{q\left(y_1\cdots,y_n| x\right)}] \\\\ =\ E_{y_1\cdots,y_n\sim q}[log\frac{p_\phi\left(y_1\cdots,y_n|\ x\right)}{q\left(y_1\cdots,y_n| x\right)}] +logp_\phi(x)\]然而,直接使用这个训练目标涉及到拟合KL散度,即 \(E_qD_{KL}(p_\phi(\cdot\mid \theta_{i-1})\parallel\ q(\cdot\mid x))\),会引入额外的计算和拟合噪音。
高效训练
为了高效训练,BFNs还进行了两个设计:为了进行simulation-free的训练,BFNs根据 精度可加性推导出了\(p_F\left(\theta_i\mid x,\alpha_i\right)\)的分布,避免从\(\theta_0\)开始逐步采样得到\(\theta_i\)来计算\(E_qD_{KL}(p_\phi(\cdot\mid \theta_i)||\ q(\cdot\mid x))\) 。
另一方面,BFNs利用李雅普诺夫中心极限定理推导出了n趋于无穷时\(L^n\left(x\right)\)的形式:
\[\lim_{n\rightarrow\infty}{L^n\left(x\right)=}L^\infty\left(x\right)=E_{p_F\left(\theta_t| x,t\right)}\alpha\left(t\right)\parallel x-E_{p_o(\hat{x}|\theta_t)}\hat{x}\parallel _2^2\]其中\(\alpha\left(t\right)=\lim_{\epsilon\rightarrow0}{\frac{\alpha_{t+\epsilon}-\alpha_t}{\epsilon}}\),\(E_{p_o(\hat{x}\mid \theta_t)}\hat{x}\)是输出分布的期望。 \(L^\infty\)对于连续或离散变量都是L2损失,提高了训练稳定性,并且可以高效计算。
总结
扩散模型在生成质量和理论完备性上保持优势,流匹配模型通过灵活加噪和高效采样实现低步数SOTA效果,而贝叶斯流网络凭借多模态建模能力成为科学领域复杂数据生成的前沿工具。未来可通过融合不同模型的优势(如流匹配的高效采样与贝叶斯流网络的多模态能力),结合理论创新与训练优化,推动生成技术在科学发现(如药物设计)和跨模态生成(视频/3D内容)领域的突破,同时通过算法改进降低计算复杂度,拓展生成模型的实际应用边界。
- Lipman, Y., et al., Flow matching for generative modeling. arXiv preprint arXiv:2210.02747, 2022.
- Graves, A., et al., Bayesian flow networks. arXiv preprint arXiv:2308.07037, 2023.
- Saharia, C., et al., Photorealistic text-to-image diffusion models with deep language understanding. Advances in neural information processing systems, 2022. 35: p. 36479-36494.
- Brooks, T., et al., Video generation models as world simulators. 2024. URL https://openai. com/research/video-generation-models-as-world-simulators, 2024. 3.
- Hoogeboom, E., et al., Simpler diffusion (sid2): 1.5 fid on imagenet512 with pixel-space diffusion. arXiv preprint arXiv:2410.19324, 2024.
- Esser, P., et al. Scaling rectified flow transformers for high-resolution image synthesis. in Forty-first International Conference on Machine Learning. 2024.
- Chen, Y., et al., F5-tts: A fairytaler that fakes fluent and faithful speech with flow matching. arXiv preprint arXiv:2410.06885, 2024.
- Jin, Y., et al., Pyramidal flow matching for efficient video generative modeling. arXiv preprint arXiv:2410.05954, 2024.
- Liu, X., C. Gong, and Q. Liu, Flow straight and fast: Learning to generate and transfer data with rectified flow. arXiv preprint arXiv:2209.03003, 2022.
- Song, Y., et al., Unified generative modeling of 3d molecules via bayesian flow networks. arXiv preprint arXiv:2403.15441, 2024.
- Qu, Y., et al., MolCRAFT: Structure-Based Drug Design in Continuous Parameter Space. arXiv preprint arXiv:2404.12141, 2024.
- Gong, J., et al., Steering Protein Family Design through Profile Bayesian Flow. arXiv preprint arXiv:2502.07671, 2025.
- Wu, H., et al., A Periodic Bayesian Flow for Material Generation. arXiv preprint arXiv:2502.02016, 2025.
- Song, Y., et al., Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456, 2020.
- Tong, A., et al., Improving and generalizing flow-based generative models with minibatch optimal transport. arXiv preprint arXiv:2302.00482, 2023.



